Zeno of Elea and the Impossibility of Motion

By Van Bryan

Zeno of Elea was a rather interesting presocratic philosopher, though that isn’t to say other presocratics were uninteresting. There were plenty of thinkers who proposed very bold, ambitious ideas in an attempt to decipher some form of truth. Zeno of Elea, however, was the most notable because of his assertion that motion, as we know it, is impossible. Not only did he make this large claim, he attempted to prove it.

Zeno was a disciple of Parmenides, who was the philosopher who went one step further, by claiming that any form of change is impossible. It is largely believed that Zeno’s arguments, later known as ‘Zeno’s Paradoxes’, were constructed as a means to support the argument of his mentor that “all is one” and that the universe is incapable of difference.

Zeno was one of the first thinkers to rely consistently on the argument of Reductio ad absurdum. This is the process of arguing that a statement is false by asserting that an absurd result would follow the acceptance of that idea. Zeno and Parmenides relied entirely on rational thought and argumentation to arrive at conclusions, as they believed very strongly that information from our senses was inaccurate and misleading.

This is probably a good position to take, because all of Zeno’s paradoxes could presumably be disproved through simple observations.

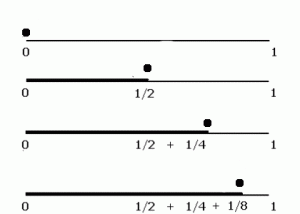
Zeno makes the argument that motion is impossible. He does this through a rather simple, eloquent, but still confounding series of arguments. Essentially, Zeno contends that before an object can reach its target, it must first achieve the halfway mark. After that, the object is obliged to traverse to the median of the remaining distance. Continuing on, it must then reach the next halfway mark again and again and again, Ad infinitum.

Zeno attempts to logically disprove motion

Another way of looking at it is to say that between point A and point B, there exists distance X, which would appear to be finite. However, it can be divided into 1/2 and then 1/4th and then 1/8th and 1/16th, and on and on forever. So distance X is actually infinite, and it is impossible to traverse infinity.

The example is often given of Achilles and a tortoise in a foot race. The tortoise gets a 100 meter head start, and Achilles will attempt to catch the tortoise. However, by the time he reaches halfway, the tortoise has moved further. Achilles will then reach the new halfway mark, but the tortoise has moved once again even further. It would appear that there are an infinite number of intermediate spots that Achilles must reach before catching the turtle, and this is triumphed as a logical impossibility.

“That which is in locomotion must arrive at the half-way stage before it arrives at the goal”- recounted by Aristotle, Physics

According to Zeno, mighty Achilles will never catch the tortoise

Maybe not surprising, there have been numerous objections to this idea that motion is impossible. Aristotle himself noted that as the distance needed to be covered shrinks, so does the time needed to traverse said distance. It was also said that Diogenes the cynic, upon hearing Zeno’s argument, attempted to disprove him by simply getting up and walking around. It is important, however, to disprove the reasoning behind Zeno’s argument, not just demonstrate a conclusion.

Some one thousand or so years later Saint Thomas Aquinas would make a counter argument by saying that:

“Instants are not parts of time, for time is not made up of instants any more than a magnitude is made of points”

The philosopher Archimedes had similarly developed “The Quadrature of the Parabola” which allowed him to arrive at a finite conclusion from the sum of an infinite amount of terms, all whose values become progressively smaller.  This idea of a converging infinity has been a popular counter argument to Zeno and his confounding paradox.

Zeno and his paradoxes have remained a popular topic for centuries. The famous paradoxes were an attempt to prove the existence of an unchanging universe, where motion and fundamental change were impossible.  It remains interesting food for thought; modern mathematicians often claim it is resolved while others may use it as a canvas to project their profound phenomenological concerns. Regardless of your position, Zeno of Elea deserves recognition for his bold assertions that have caused countless thinkers after him to scratch their heads in puzzlement.